About convolutional neural network
其实关于CNN很早之前就已经知道了它大概是什么原理,以及它为何比人为提取的特征用来训练得到的效果更好。可以说CNN几乎终结了计算机视觉领域靠人为提取特征的时代(也就是我刚开始学习进入这领域的时候😂)。
但这里我想从头梳理一遍,以普通的神经网络为切入点,换个角度研究下CNN。
-
总体而言,CNN和普通的神经网络的区别:
First of all, the layers are organised in 3 dimensions: width, height and depth. Further, the neurons in one layer do not connect to all the neurons in the next layer but only to a small region of it. Lastly, the final output will be reduced to a single vector of probability scores, organized along the depth dimension.
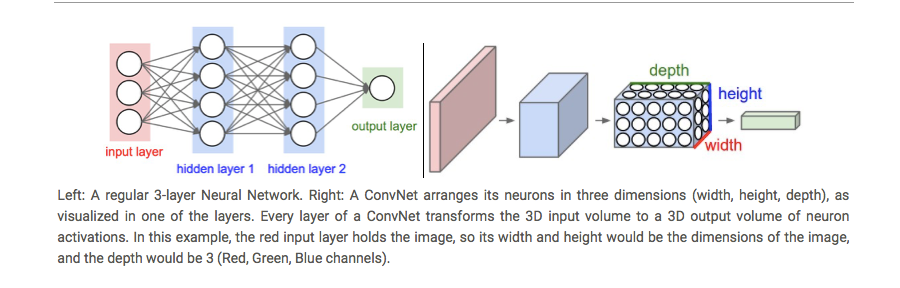
-
CNN中一共有这么几种layer:
- INPUT [32x32x3] will hold the raw pixel values of the image, in this case an image of width 32, height 32, and with three color channels R,G,B.
- CONV layer will compute the output of neurons that are connected to local regions in the input, each computing a dot product between their weights and a small region they are connected to in the input volume. This may result in volume such as [32x32x12] if we decided to use 12 filters.
- RELU layer will apply an elementwise activation function, such as the max(0,x) thresholding at zero. This leaves the size of the volume unchanged ([32x32x12]).
- POOL layer will perform a downsampling operation along the spatial dimensions (width, height), resulting in volume such as [16x16x12].
- FC (i.e. fully-connected) layer will compute the class scores, resulting in volume of size [1x1x10], where each of the 10 numbers correspond to a class score, such as among the 10 categories of CIFAR-10. As with ordinary Neural Networks and as the name implies, each neuron in this layer will be connected to all the numbers in the previous volume.
INPUT就不说了,CONV是卷积层,也是CNN的核心,卷积层最大的特点(相比于一般的NN)是它只关注输入的局部信息;RELU层的作用应该和普通的NN差不多:注入一些非线性的因素;POOL是池化层,作用类似于降采样,降采样后再输入到下一层卷积层,那么更全局的信息就被关注到了,可以有效的降低overfitting(试想下如果只给你看树叶的纹路,鬼能看得出这是什么树)和提高robust(即使图像有一些平移或旋转,降采样后可能是一样的,所以没有太大影响);FC是全连接层,可以理解为就是把之前各种卷积、池化等操作之后的输出展开为一维的向量,再输入到了一个普通的神经网络中(普通的NN中每一层都是全连接的)。
-
关于卷积:卷积其实就是加权叠加,在图像处理中通常会选用一个较小的矩阵模板(也叫描述子或卷积核,比如一个3x3的矩阵)来对图像中的每一个像素和其周围部分像素进行加权叠加计算,从而得到一个全新的图像(对于图像边缘的像素,一般会采取镜像操作来填充一些图像外的点来计算,以保证卷积过后的图像尺寸不变,比如要在图像
[5,0]处和3x3的矩阵进行卷积,那么我们会用[5,1]处的图像像素来填充到[5,-1]的位置,然后就可以进行卷积啦)。图像卷积在图像处理中的应用非常广泛,比如图像的去噪、锐化、模糊化、边缘检测等等,这些操作其实都是在图像上进行卷积,所不同的是它们使用的卷积核不同罢了。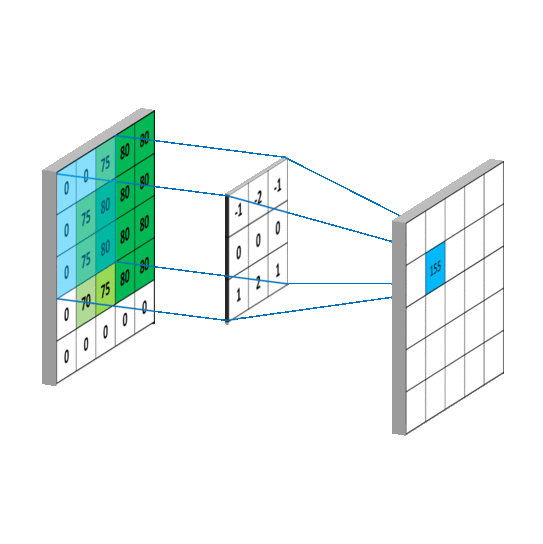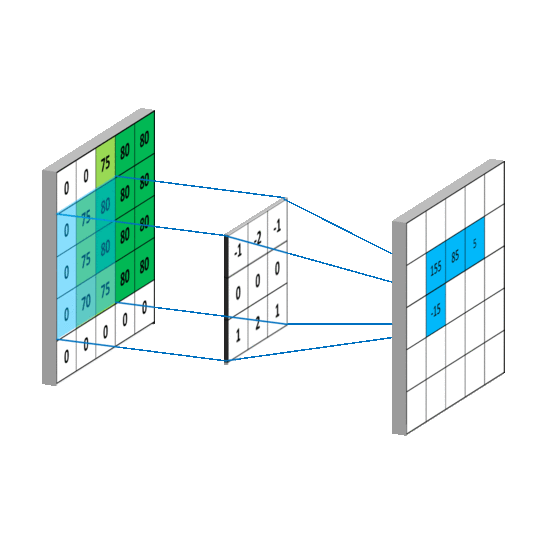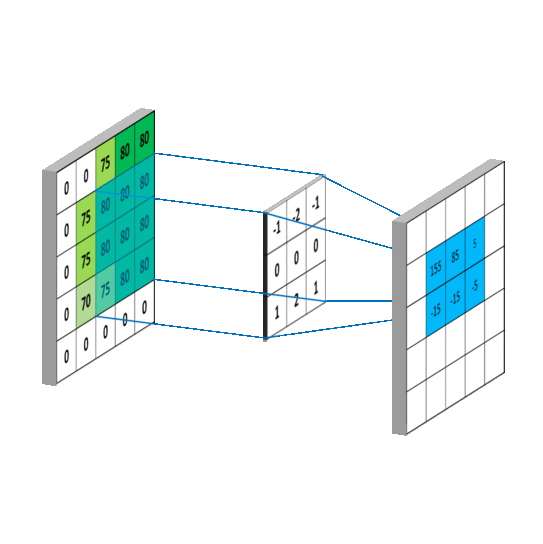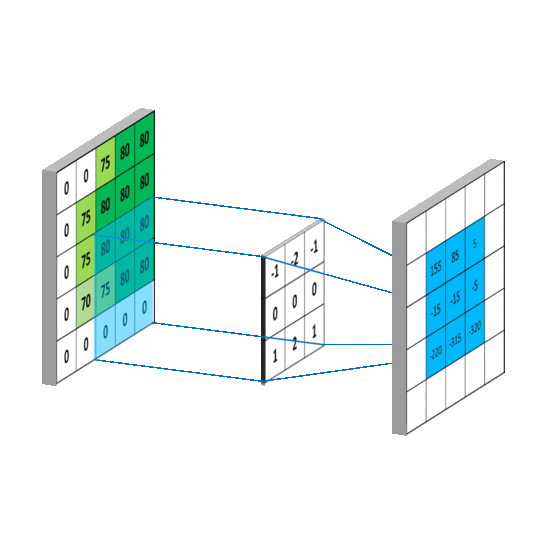
-
关于卷积,换个角度:
卷积定理指出,函数卷积的傅里叶变换是函数傅里叶变换的乘积。即,一个域中的卷积相当于另一个域中的乘积,例如时域中的卷积就对应于频域中的乘积。
因此对图像的局部做卷积就相当于在图像频域中做乘积?(我对图像频域这块理解不深,只记得图像高频代表了图像的一些细节特征,因此可以通过低通滤波器来对图像进行降噪(过滤掉特别高频的部分好像也类似于对图像做了平滑卷积的操作?))
-
把卷积的公式展开:设3x3的卷积核W,其中Wij表示其中第i行j列的参数,输入为X,同样Xij表示输入的第i行j列的值,那么其中一个卷积结果可以表示为:
O22 = W11*X11 + W12*X12 + W13*X13 + W21*X21 + W22*X22 + W23*X23 + W31*X31 + W32*X32 + W33*X33最终的输出还会再加上一个偏置b。如果把这里的X和W看做一个一维的向量而不是二维矩阵,是不是感觉突然熟悉?普通的神经网络中的神经元的也有这样的计算,只不过它的输入是上一层的所有的输出,而这里的输入只选取了上一层输出的一部分。所以,这就能理解为啥CNN中神经元是按照三维空间排列的,每一次卷积运算都对应了一个神经元,并且对卷积层而言这些神经元的激活函数仍是线性的(y=x嘛,当然也可以说是没有激活函数)。
-
对于深度大于1的输入,卷积核也要有相同的深度,比如深度为11x11x3,那么卷积核就需要是5x5x3或3x3x3等等。计算卷积时,不同深度的输入分别和对应深度的卷积核进行二维卷积计算,最终的输出为各个深度在相同位置的卷积结果之和。因此,对于卷积层而言,输出的深度就代表了卷积核的数目。(其实就是三维的卷积操作,只不过我们可能对二维平面上的卷积更熟悉一些,所以这里详细说一下三维是怎么操作的。)
-
具体实现上,CNN(不考虑全连接层)和普通的深度神经网络(以下用DNN代指)的区别在于:
- DNN的每一层的输出为1xN的向量;而CNN每一层的输出为MxNxD的矩阵(可以看做是D个MxN的二维矩阵)。
- DNN的每一层都包含了很多的神经元,而每个神经元则含有自己的权重(weights),通过对损失函数反向传播,我们计算出每个神经元权重的梯度,进而修改神经元的权重来降低损失函数的输出;而CNN的每一层也有很多神经元,但它们会共享同一套权重(使用了相同的卷积核),同样通过对损失函数反向传播,来修改神经元共享的权重(卷积核)。
- DNN的层与层之间是全连接的,因此神经元可以任意排布;而CNN中卷积操作使神经元只和上一层的一部分神经元产生了连接,并且由于卷积是和空间位置相关的,所以神经元的空间排布直接影响到下一层的输出,因此位置不能随意改变。
- CNN中的超参数(hyperparameter)和DNN不太一样:CNN中卷积层需要确定卷积核的尺寸、卷积核的数目、卷积核滑动的步幅(stride)、输入边缘填补的方式(补零、镜像等),池化层需要确定池化的尺度;而DNN中则需要确定的是,每一层的神经元数目和神经元的激活函数。层数、训练迭代次数、学习率和损失函数是两者都存在的超参数。 (关于参数和超参数:参数是随着训练会不断改变的变量,比如神经元中的权重和偏差,而超参数则是用于确定模型的一些参数,不会随模型训练而改变,比如学习率、迭代次数、层数、每层神经元的个数等。)
-
关于参数共享,CNN之所以用同一个卷积核来对输入进行卷积操作,Standford教程里是这么说的:
It turns out that we can dramatically reduce the number of parameters by making one reasonable assumption: That if one feature is useful to compute at some spatial position (x,y), then it should also be useful to compute at a different position (x2,y2).
If detecting a horizontal edge is important at some location in the image, it should intuitively be useful at some other location as well due to the translationally-invariant structure of images.
只能说是一种直觉和猜想吧,不过也确实说得通,因为我们是期望将图像中的某个目标平移后还能照样检查或识别出来的,平移后目标区域就是其他的神经元来对它做卷积了,那这个神经元由于使用了相同的卷积核,因此可以和之前那个神经元卷积得到相同的特征。另外,从计算性能上来考虑,共享参数也是有必要的。
Note that sometimes the parameter sharing assumption may not make sense. This is especially the case when the input images to a ConvNet have some specific centered structure, where we should expect, for example, that completely different features should be learned on one side of the image than another. One practical example is when the input are faces that have been centered in the image. You might expect that different eye-specific or hair-specific features could (and should) be learned in different spatial locations. In that case it is common to relax the parameter sharing scheme, and instead simply call the layer a Locally-Connected Layer.
感觉在这种情况下,还使用共享参数那套框架,但使用更多的神经元(卷积核)和更多的层数应该也能达到一样好的效果,只不过在不同区域提取不同的特征可以节省神经元(计算量)。
-
关于池化层:现在比较流行方式的是max pooling,曾经流行的还有average pooling、L2-norm pooling等(猜测max pooling效果更好是因为它是非线性的操作?)。
-
在卷积层选择比较大的stride也能达到和池化差不多的作用,因此某些情况下池化层并不是必须的。
-
关于反向传播:
- 由于正向传播时CNN在全连接层的输入是一组1x1xD的神经元,即可以看做是1xD的向量输入到DNN中,因此反向传播全连接层及之后的部分和DNN的反向传播相同。
- 池化层的反向传播,以max pooling为例,我们知道max运算的反向传播的结果为,正向传播时输入的最大值的梯度等于输出的梯度,其他输入的梯度为0。比如正向传播的输入为
[[1,8],[3,5]],反向传播得到的输出的梯度为g,则反向传播可得输入部分的梯度为[[0,g],[0,0]]。(其实也没啥特殊的,就是对max运算进行反向传播而已) - 卷积层的反向传播,其实就是一个线性函数的反向传播,和DNN中的神经元反向传播类似。
以上,反向传播只和具体的运算操作有关,不管是CNN、DNN还是XXXNN,反向传播都一个样。
-
CNN一般的结构:
INPUT -> [[CONV -> RELU]*N -> POOL?]*M -> [FC -> RELU]*K -> FCwhere the
*indicates repetition, and thePOOL?indicates an optional pooling layer. Moreover,N >= 0(and usuallyN <= 3),M >= 0,K >= 0(and usuallyK < 3).- 最后那部分
[FC -> RELU]*K -> FC其实就是含有K个隐层的DNN(且隐层激活函数为ReLu,输出层激活函数为线性函数)。 - 卷积层永远后面都会紧跟一个ReLu层,这是因为两个相邻的卷积层是可以合并成一个卷积层的,所以设计两个连续的卷积层没有意义,还浪费训练更多的参数。
- 最后那部分
-
综上,CNN可以看做是一种神经网络的特例,特殊在于神经元的参数共享和局部连接。特殊化意味着它对某一类问题会更加有效(统计学上来说就是减少了假设空间,从而使训练得到理想模型的概率提高了),但对于解决其他的问题可能完全无效。换句话说,使用更加通用的DNN理论上应该也能够解决CNN能解决的问题,但代价可能是需要更多的神经元以及多得多得多的参数要训练。

Comments