1. 学习率是指每次进行梯度下降时，各个参数按照梯度进行调整的比例。学习率越高，则每次迭代参数调整得越大，训练的效率也就越高；但学习率太高，可能会导致训练无法收敛到最佳。

    It will turn out that the setting of the step size is very imporant and tricky. Small step size will make your model slow to train. Large step size will train faster, but if it is too large, it will make your classifier chaotically jump around and not converge to a good final result.

  2. 为了达到更好的训练效果，学习率在训练过程一般都会用一些算法来动态地调整，比如说让梯度一直都很小的weight偶尔可以以较大的学习率来改变下。现在用的比较多的是Adam方法（参考这里）。

  3. 目前，神经网络的隐层的激活函数一般选择ReLu函数（sigmoid函数或tanh函数也可以，但存在vanishing gradient问题，会导致某些情况下训练效率很低），而输出层则一般会根据需求来定：

    • 用于回归一般选择线性函数即可（因为没有边界的要求）
    • 用于分类则使用softmax函数或sigmoid函数

    (参考这里)

  4. 激活函数选择ReLu函数还有一个原因是它的值的计算以及梯度的计算都非常简单，对于深度的神经网络而言减少训练的计算量还是挺重要的。（ReLu函数存在dying ReLu problem，但通过简单地修改可以克服这个问题，参考这里）

  5. 同样学习率、同样的训练迭代次数下，如果训练得到的模型预测误差仍不同，则还有可能是每次训练的权重的初始值不同且迭代次数不足导致。

  6. 我们是根据损失函数（loss function）来反向传播并计算梯度的，而损失函数一般分为两部分：

    J(w) = L(w) + R(w)

    其中L(w)计算的是预测值与真实值的差距，可以理解为实实在在的损失，R(w)是所有和输入的feature相关的权重有关的函数，目的是防止某些权重过大，导致某些feature的话语权太大压制了其他的输入（即Regularization），因为真实世界中收集得到的输入总会有噪音，一旦噪音的话语权太大就会导致模型预测不准确（即overfitting）。

  7. 一些损失函数对于网络的输出是有要求的（或者说，一些网络的输出限制了我们对于损失函数的选择）。比如Hinge Loss，它的损失只有在输出大于等于+m或小于等于-m（m为margin，即SVM中两个超平面的距离的一半）时为0，因此如果神经网络的输出层激活函数使用的是sigmoid函数，那计算得到的损失就是不准确的（sigmoid函数输出为0到1区间）。

  8. 适当地使用dropout可以提高训练的效率、减少训练模型的overfitting。所谓dropout是指将一层神经网络中的一部分输出丢弃掉并置为0再输入到下一层神经网络中。下图是一个CNN的网络分别不使用dropout及对其中某些层后面添加dropout得到的训练效果（MNIST训练集），可以看到使用dropout后，在同样的迭代次数下，训练效果要好了很多。 不使用dropout，分类准确率为0.5982 添加了dropout，分类准确率达到0.9046

  9. 神经网络同一层中的神经元（neuron）的参数（weights）的初始值不要一样，因为如果有两个神经元的参数值是一样的，那么无论怎么进行训练（学习率也保持一致的话），得到的还是两个一模一样的神经元，其实就和只有一个神经元的效果是一样的了（即一个神经元的输出*2）。

  10. 神经网络同一层中的神经元数目的影响（以ReLu激活函数为例）：我们考虑一个只有一个隐层的神经网络，该隐层的每一个神经元的输出都是一个拥有一个拐点的分段函数，那么输出层的每个神经元的输出是什么样的呢？它的输出其实也是一个分段函数，可以看成它是前面一层的所有输出的叠加（见下图），理论上它的拐点数目即等于前面一层所有神经元输出的拐点数之和。因此，增加神经元的数目可以使神经网络去拟合更加复杂的“曲线”，解决更加复杂的问题。 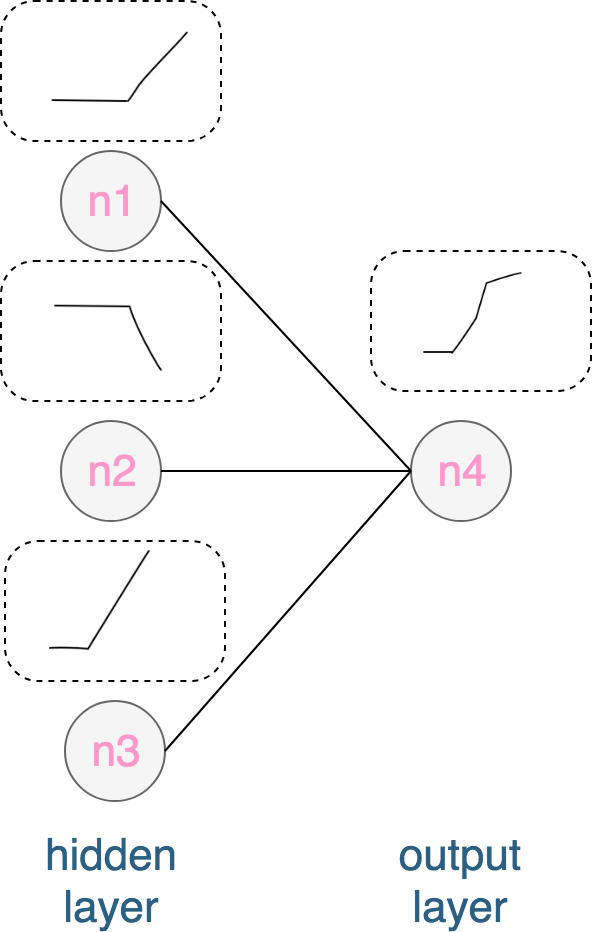神经元数目的影响

  11. 神经网络隐层数目的影响（以ReLu激活函数为例）：假设每一层有三个神经元，那么第一层的每个神经元的输出为拥有一个拐点的分段函数，第二层的输出则拥有了3个拐点，第三层的输出在前一次的基础上最多可以得到3*3=9个拐点的函数，以此类推（见下图）。所以，增加神经网络的深度（即增加隐层的数目），同样可以让神经网络去拟合并解决更复杂的问题，并且增加深度要比单纯地增加某一层的神经元数目的“效率”要高（试想如果只有一层隐层，我们需要9个神经元才能达到和有两层隐层，且每层3个神经元的效果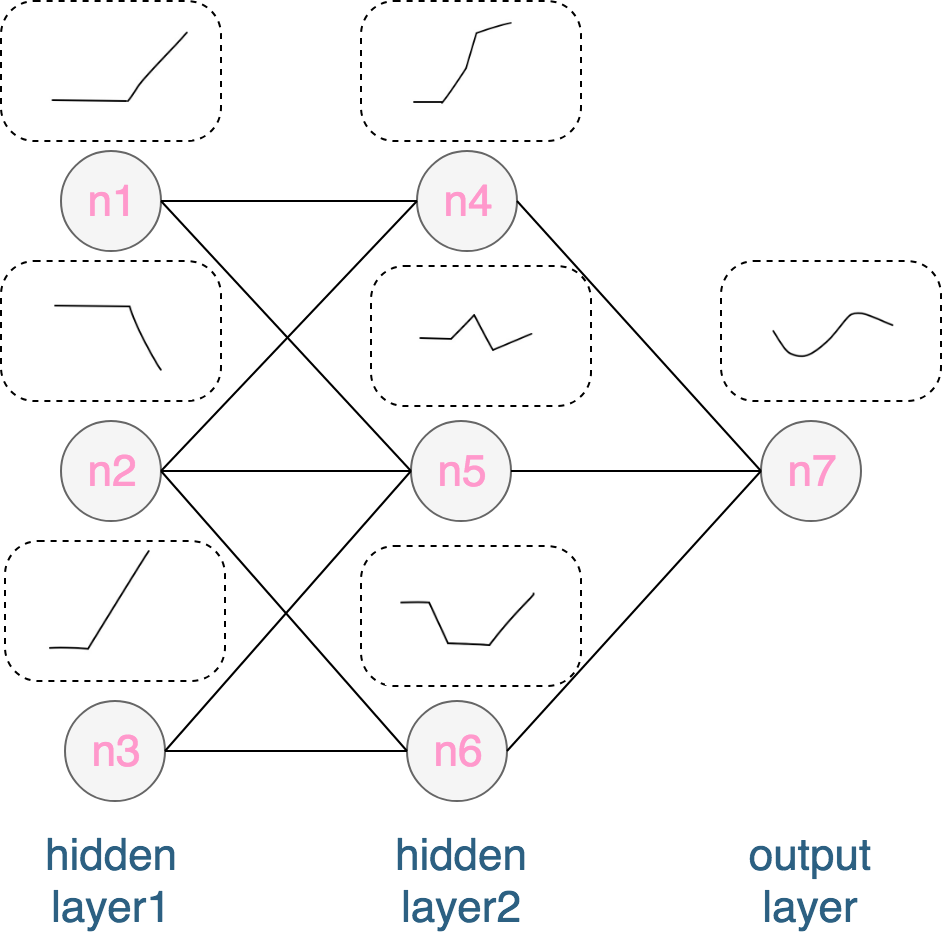）。 隐层数目的影响

  12. 目前来说，只要隐藏数目大于1，则可以称之为深度神经网络。至于为何深度神经网络训练得到的效果会好于浅层的神经网络，似乎现在还没有定论。或许，只要浅层的神经网络中的神经元足够多，也能达到深度神经网络一样的效果也说不定（但参考上面第10和第11条目，达到一样的效果所需要的神经元会非常多）。或许，除了神经元数目之外，还有其他的因素导致了深度的神经网络效果更好（参见这篇回答）。

  13. 对于多类分类问题，我们可以用多个二类分类器来实现，也可以直接打造一个多类分类器。神经网络对于多类分类其实很好实现，因为输出层本来就可以有多个神经元，我们可以让每一个输出的神经元代表一个类别，比如[0.1, 0.8, 0.2]表示类别2的概率比较高。另外一个思路是把每个输出层神经元看做一个二类分类器，比如[-1, -1]表示类别1，[-1, 1]表示类别2，[1, -1]表示类别3，[1, 1]表示类别4。

  14. 如果神经网络的输出层存在多个神经元，那么每个神经元是可以使用不同的loss function的（根据需求来定，参考这里），并且最后可以通过加权的方式得到最终的loss。

  15. 关于batch size，是指某一次迭代输入到神经网络训练的样本数量。之所以存在batch size的概念，一是因为对于海量的训练数据，内存不够用了，没办法一次性把所有的训练样本都输入到神经网络中进行正向和反向传播，二是因为有时候选取较小的batch size可以避免过拟合或损失陷入鞍点。一些相关的概念：

  • one epoch = one forward pass and one backward pass of all the training examples
  • batch size = the number of training examples in one forward/backward pass. The higher the batch size, the more memory space you’ll need.
  • number of iterations = number of passes, each pass using [batch size] number of examples. To be clear, one pass = one forward pass + one backward pass (we do not count the forward pass and backward pass as two different passes).

（参考这里和这里）